[이산수학 - 2강] 명제와 명제 논리 / 술어 논리와 추론
한국방송통신대학교 이산수학 강의 2강을 듣고 공부한 내용을 정리한 포스팅입니다
2강의 학습목표
- 명제와 명제가 아닌 것을 구분할 수 있다
- 다양한 논리연산자의 역할을 이해하고 합성명제의 진리값을 판별할 수 있다
- 조건명제와 쌍조건명제를 구분하고 진리값을 찾아낼 수 있다
- 서로 다른 두 명제의 논리적 동치 여부를 판별할 수 있다
- 추론규칙 또는 벤 다이어그램을 이용하여 타당한 추론을 판별할 수 있다
- 명제 (Proposition)
참과 거짓을 구별할 수 있는 문장이나 수학적 식을 명제라고 한다. 명제가 타당할 경우 명제가 참(true)이라고 하며, 명제가 타당하지 않을 경우 거짓(false)라고 한다. 이 때 참과 거짓을 명제의 진리값이라고 한다.
종류
합성 명제, 조건 명제, 쌍조건 명제, 항진명제, 모순명제
- 논리 연산
합성 명제 (compound proposition)
하나 이상의 명제와 논리연산자들이 결합되어 만들어진 명제를 합성명제라고 한다
논리 연산자
논리 연산자의 종류에는 논리합, 논리곱, 부정, 배타적 논리합이 있다
- 논리합 (or, ∨)
'또는'의 의미를 가지고 있는 논리 연산자. '∨' 로 표현한다.
논리합 p ∨ q의 진리값은 p와 q 중 하나라도 참일 경우 참이된다. 진리표는 아래와 같다
| p | q | p ∨ q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
- 논리곱 (and, ∧)
'그리고'의 의미를 가지고 있는 논리 연산자. '∧' 로 표현한다.
논리곱 p ∧ q의 진리값은 p와 q 모두 참일 경우만 참이 된다. 진리표는 아래와 같다
| p | q | p ∧ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
- 부정 (not, neation, ~, ¬, ` )
명제의 진리값을 반대로 하는 연산자이다. 1항 연산에만 사용 가능하기 때문에 진리표는 아래와 같다
| p | ~p |
| T | F |
| F | T |
- 배타적 논리합 (exclusive or, xor, ⊕)
논리합에서 모두 참일 경우를 배제하는 연산자이다. '⊕'로 표현한다
즉 배타적 논리합 p ⊕ q의 진리값은 p와 q 중 하나가 참일 경우만 참이 된다. 진리표는 아래와 같다
| p | q | p ⊕ q |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
- 조건 명제와 쌍조건 명제
조건 명제 ( conditional proposition, → )
명제 p와 q가 있을 때, 명제 p가 조건의 역할을 수행하고 명제 q가 결론의 역할을 수행하는 경우 조건 명제라고 한다.
조건이 참이면 결론에 따라 참과 거짓이 나뉘지만 조건이 거짓일 경우 결론이 참이든 거짓이든 조건 명제의 진리값은 참이 된다.
진리표는 아래와 같다
| p | q | p → q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
쌍조건 명제 ( biconditional proposition, ↔ )
명제 p와 q가 있을 때, 명제 p와 q가 조건의 역할과 결론의 역할을 동시에 수행하는 경우 쌍조건 명제라고 한다.
쌍조건 명제 p ↔ q는 ( p→q ) ∧ (q→p) 로 분해할 수 있으며 p↔ q 는 ~(p⊕q) 와 같다.
진리표는 아래와 같다.
| p | q | p → q | q → p | p ↔ q |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
- 동치 (equivalence)
논리적 동치 (logical equivalence)
두 명제 p와 q가 논리적으로 동등하면 (항상 동일한 진리값을 가지면) 논리적 동치라고 하고 p ≡ q로 표시한다
역, 이, 대우
조건명제 p → q 가 있을 경우
- 역 (converse) : q → p
- 이 (inverse) : ~p → ~q
- 대우 (contrapositive) : ~q → ~p (조건 명제와 그에 대한 대우는 항상 논리적 동치 관계다)
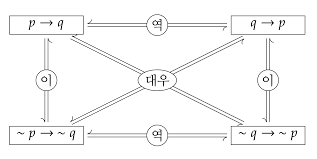
논리적 동치법칙
항진명제와 모순명제
- 항진명제 (tautology) : 항상 참인 명제
- 모순 명제 (contradiction) : 항상 거짓인 명제
- 술어 논리 (predicate logic)
명제 논리와 술어 논리
위에서 다룬, 명제 단위의 참과 거짓에만 관심을 가지는 것을 '명제 논리'라고 한다. 그러나 이는 한계가 있다. 예를 들어
'모든 사람은 죽는다', '소크라테스는 사람이다' 는 두 개의 명제가 있다 해도 논리 연산자로 어떻게 연결 하든 명제 논리만으로는 '따라서 소크라테스는 죽는다'는 당연한 사실을 추론할 수 없다.
그러나 술어 논리는 명제를 술어와 주어로 분리하여 술어(주어) 의 형태로 표현하기 때문에 주어와 술어 사이에 더 세밀한 표현을 할 수 있다. 이 덕분에 위에서 명제 함수가 가진 한계를 극복 할 수 있다. 예를 들어 '모든 사람은 죽는다' 는 명제는 '∀x{사람(x) → 죽는다(x)}' 는 술어 논리식으로 표현 가능하다. 또 '소크라테스는 사람이다'는 명제 또한 '사람(소크라테스)' 라는 술어 논리식으로 표현 가능하니 '소크라테스는 죽는다'는 명제 또한 '죽는다(소크라테스)' 라는 술어 논리식으로 도출할 수 있다.
명제 함수 (propositional function)
위의 술어 논리 식에서 사용한 것과 같이 '변수의 값에 의해 함수의 진리값이 결정되는 문장이나 식을 '명제 함수'라고 한다. 이 명제 함수를 명제로 만들기 위해 값을 지정하는 방법에는 두가지가 있다
- 변수의 값을 명시해준다
- 변수의 범위를 제시한다
이 때 변수의 영역을 '정의역'이라고 하고 변수의 범위를 제시할 때 사용하는 것을 '한정자'라고 한다
한정자 (quantifier)
- 전체한정자(universal quantifier) : 전체 한정자는 '모든'을 의미하며 '∀x' 와 같이 표현한다. ∀xP(x)와 같이 사용되고 이에 대한 진리값이 참일 경우에는 정의역의 모든 x에 대해서 P(x)가 참임을 의미한다. 예를 들어 P(x)가 'x는 실수이다' 이고 x의 정의역이 양수일 경우 ∀xP(x)의 진리값은 참이고 모든 양수 x는 실수라는 의미가 된다.
- 존재한정자 (existential quantifier) : 존재 한정자는 '존재한다'를 의미하며, '∃x' 와 같이 표현한다. ∃xP(x)와 같이 사용되고 이에 대한 진리값이 참일 경우에는 정의역의 어떤 x에 대해서 P(x)가 참임을 의미한다. 예를 들어 (P(x)가 'x는 무리수이다' 이고 x의 정의역이 유리수일 경우 ∃xP(x)의 진리값은 거짓이 되고 어떤 유리수 x도 무리수가 아니라는 의미가 된다.
타당성 검사
위와 같이 한정자가 사용된 명제함수의 타당성을 분석하기 위해 벤 다이어그램을 사용할 수 있다. 이는 매우 직관적이다.
예를 들어 '영희는 서울에 있다'와 '서울은 한국에 있다'는 두 명제를 바탕으로 '영희는 한국에 있다'는 결론을 도출한 경우 이것이 타당함은 벤 다이어그램을 통해 아래와 같이 나타낼 수 있다.
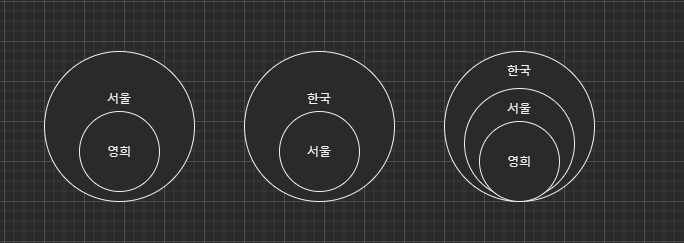
- 추론 (inference)
추론이란
참으로 알려진 명제를 기초로 하여 다른 명제를 유도해 내는 과정을 추론이라고 한다. 이 때 결론의 근거를 제공하는명제를 전제 (premise)라고 하며 새로 유도된 명제는 결론 (conclusion)이라고 한다. 추론은 하나 이상의 전제와 하나의 결론으로 구성되고 기본적으로 논리적 동치를 이용한다
유효추론
전제를 참이라고 가정하였을 때 결론이 항상 참이 되는 추론을 유효 추론이라고 한다.
예를 들어 (( p → q ) ∧ ( q → r )) → ( p → r ) 로 표현할 수 있는 삼단 논법은 대표적인 유효 추론이다.